684。冗余连接
难度:中等
>>主题:深度优先搜索,广度优先搜索,联合查找,图形
在这个问题中,一棵树是连接且没有循环的无向图。
>您获得了一个图形,该图是从1到n标记的n个节点开始的树,并增加了一个边缘。添加的边缘具有从1到n选择的两个不同的
的顶点,并且不是已经存在的边缘。该图表示为长度为n的数组边缘,其中边缘[i] = [ai ,bi]表明节点ai 返回可以删除的边缘,以便结果图是n节点的树。如果有多个答案,请返回在输入。
>
>示例1:
>输入: edges = [[1,2],[1,3],[2,3]]
>输出: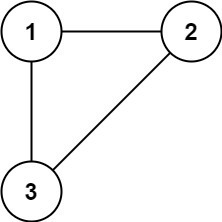 [2,3]
[2,3]
- >>示例2:
>输入:
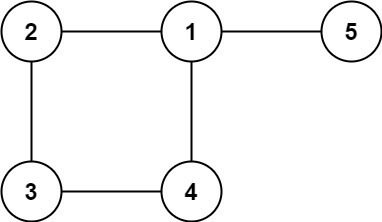
edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
[1,4]
- >约束:
- >
-
3
n == edge.length
edges [i] .length == 2
1 i i
- i
- a
- i
- i
- >
没有重复的边缘。给定的图是连接的。 - 解决方案:
- 问题要求我们确定图形中的边缘,可以将图形转换为有效的树。树是连接和无环的无向图。给我们一个图形,该图是从树开始的,但通过添加一个额外的边缘进行了修改。我们的目标是找到并返回这个额外的优势。
-
关键点
!= b
冗余连接
>
该图是未取向
和
删除冗余边缘后所得的图形必须没有周期。
答案应返回输入中出现的
最后一个
的边缘,如果有多个有效的解决方案。
由于单个额外的边缘,该图最多可以具有一个周期。
-
方法
该方法涉及使用>深度优先搜索(dfs)来检测周期:
-
>邻接列表表示:
- >使用邻接列表来表示图形。该结构适合有效地执行df。
通过dfs
循环检测:
在将边缘添加到图表之前,请使用dfs检查边缘两个顶点之间是否已经有一个路径。如果有的话,添加此边缘将形成一个周期。
-
返回边缘:
- 如果检测到一个周期,请返回当前边缘作为冗余连接。
-
计划
解析输入边缘。- 维护一个邻接列表以动态跟踪图形的连接。
- 对于每个边缘:
使用递归dfs函数检查两个顶点之间的路径是否存在。
- 如果存在路径,请返回边缘作为冗余连接。
否则,将边缘添加到邻接列表中。
如果找不到冗余边缘,则返回空结果(尽管这不会按照问题的限制发生)。
>让我们在php中实现此解决方案:
684。冗余连接
<?php
/**
* @param Integer[][] $edges
* @return Integer[]
*/
function findRedundantConnection($edges) {
...
...
...
/**
* go to ./solution.php
*/
}
/**
* Helper function to perform DFS and check connectivity
*
* @param $src
* @param $target
* @param $visited
* @param $adjList
* @return bool
*/
private function isConnected($src, $target, &$visited, &$adjList) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$edges1 = [[1,2],[1,3],[2,3]];
$edges2 = [[1,2],[2,3],[3,4],[1,4],[1,5]];
print_r(findRedundantConnection($edges1)) . "
"; // Output: [2,3]
print_r(findRedundantConnection($edges2)) . "
"; // Output: [1,4]
?>
解释:
- dfs实现
-
- 从一个节点开始,然后递归访问其邻居。
- 如果在遍历期间达到目标节点,则存在一条路径。
使用访问的数组避免重新访问节点。
- :
:
edge addad
如果在边缘的顶点之间不存在路径,请将边缘添加到邻接列表中,然后继续进行下一个边缘。
冗余边缘
:
-
如果已经存在路径,请在形成周期时返回当前边缘。
- >输入
示例演练
示例1:
:edges = [[1,2],[1,3],[2,3]]
- :
>将邻接列表初始化为[]。- 处理边缘:
添加[1,2]→图:{1:[2],2:[1]}
-
检查[2,3]:dfs找到路径→返回[2,3]。
- >输出
:[2,3]
示例2:
步骤
添加[1,3]→图:{1:[2,3],2:[1],3:[1]}
> input
:edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
:
>将邻接列表初始化为[]。
处理边缘:
添加[1,2]→图:{1:[2],2:[1]}
- 添加[2,3]→图:{1:[2],2:[1,3],3:[2]}
- 添加[3,4]→图:{1:[2],2:[1,3],3:[2,4],4:[3]}
- 检查[1,4]:dfs找到路径→返回[1,4]。
- 输出
:[1,4]
时间复杂性
dfs traversal
:
对于每个边缘,我们执行一个dfs来检查连接。
最差的情况:
o(v e)
,其中
v
- 是顶点的数量,
- e
- 是边的数量。
总复杂度
:
由于我们为每个边缘执行dfs,因此总体复杂性为
o(e×(v e))
。
-
空间复杂度
:
- o(v e) 。。
访问阵列:o(v)。
总计:
>邻接列表:
o(v e)
- 。
输出示例
-
示例1:
> input :[[1,2],[1,3],[2,3]]
>
>
-
- :[2,3]
示例2:
>输出
github
以上就是冗余连接的详细内容,更多请关注php中文网其它相关文章!