解析PHP如何实现有趣的汉诺塔算法

2021-07-21

解析PHP如何实现有趣的汉诺塔算法

昨天研究了一天汉诺塔算法都没搞懂，感觉自己智商被碾压了，还不如《猩球崛起》中的那一只猩猩！！！

起源

传说最早发明这个问题的人是法国数学家『爱德华·卢卡斯』。

在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

这个传说有很多的变本具体是谁就不得而知了，但是留下的数学问题却是很经典的。

其留下的数学知识：金片的个数和移动步数的关系为 2^n - 1。

1个金片的移动次数 2的1次方减1
2个金片的移动次数 2的2次方减1
3个金片的移动次数 2的3次方减1
…
个金片的移动次数 2的n次方减1

若传说属实，僧侣们需要 2^64 - 1 步才能完成这个任务；假设他们每秒移动一个金片，就需要 5849 亿年才能完成。整个宇宙现在也不过 137 亿年，所以宇宙毁灭还早…（闲的无聊，我还真计算了一下，如下图）

计算结果

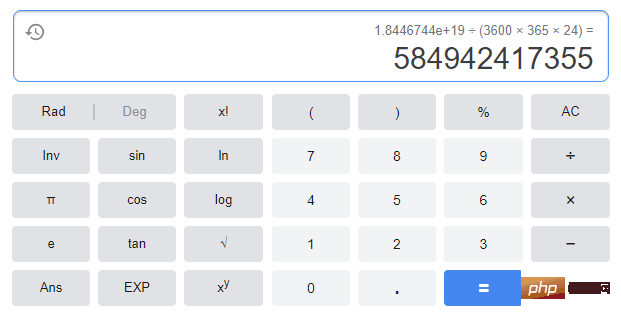
基本规则

汉诺塔算法有2个基本条件，假设移动的是盘子。

1.每次只能移动一个盘子。
2.小盘子必须要在大盘子的上面。

分析

假设本次游戏有3根柱子，分别是 A， B， C。其中一根上已经有排序好的盘子N个，最大的在最下面，依次向上盘子越来越小，另外2根空柱子。

初始状态如下图：

初始状态

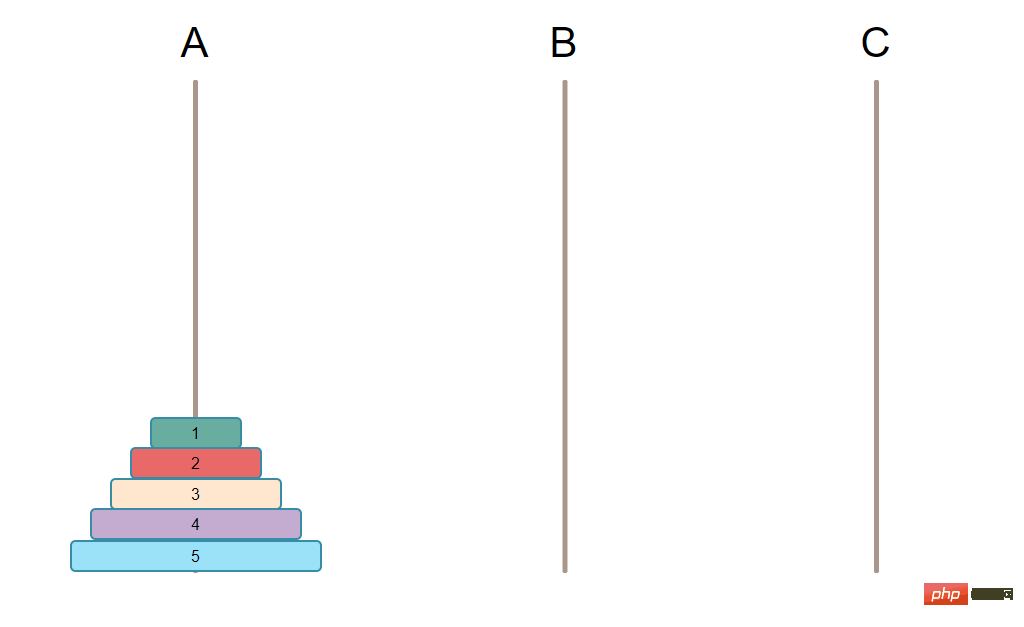
需要实现的最终目标是把柱子上所有的盘子都移动到另外一根柱子上。【推荐学习：PHP视频教程】

目标结果

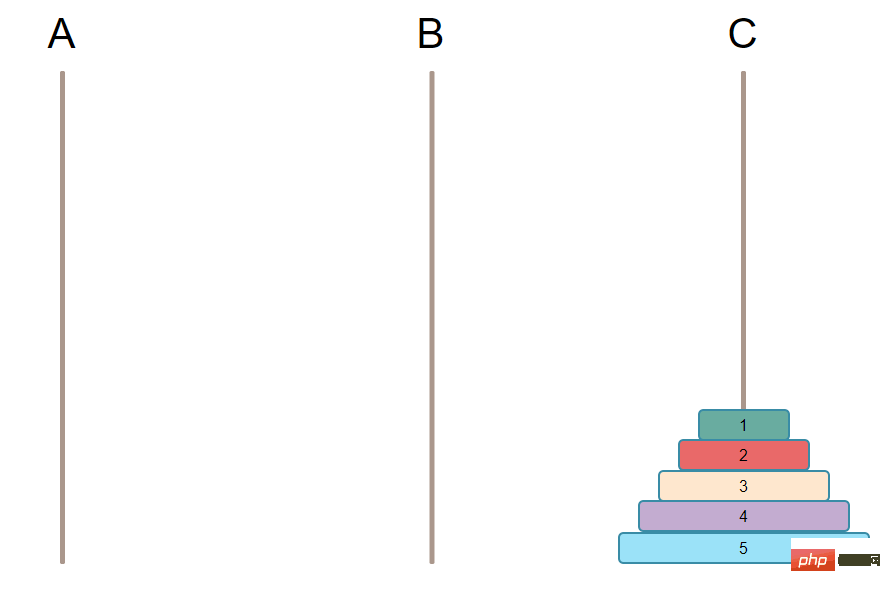
实现的大概思路：

抛开脑子里想着的每一步要怎么走，这个很复杂，脑容量估计不够，先想最简单粗暴的解决逻辑。
要满足大盘子在下的基本条件，肯定需要先把A上最大的盘子空出来，然后把最大的盘子放到C柱子上。假设最大的盘子编号是N。
因为要移动到C，要实现第一步，肯定需要把 N-1 个盘子都搬移到B柱子上，只有这样第N个盘子（也就是最大的盘子）才能移动到C柱子上。
把 N-1 个盘子移动到B柱子上，因为要满足条件大的在下，小的在上，所以这 N-1 个盘子在B柱子上也是顺序的。
最后把这 N-1 个盘子从B柱子上移动到C柱子上完成最终目标。

概括下：

第一步把A上 N-1 个盘子移动到B上。

为什么要先把 N-1 个先移动到B上？你看，因为你最终实现的是把A上全部的盘子都移动到C上，顺序又不能变，只能是大的在下，小的在上。那你肯定需要先把最大号的移动到C，不然的话就不满足条件了。

要从A上移动最大号盘子到C上，肯定需要把A上最大号盘子空出来，也就是最大号盘子上面的所有盘子都要搬移走。而你只有3根柱子，C上肯定是不能有别的盘子把，不然你就又不满足条件了，所有这 N-1 个盘子只能放到B上，而且还是有序的。也就变成了下图：

第一步

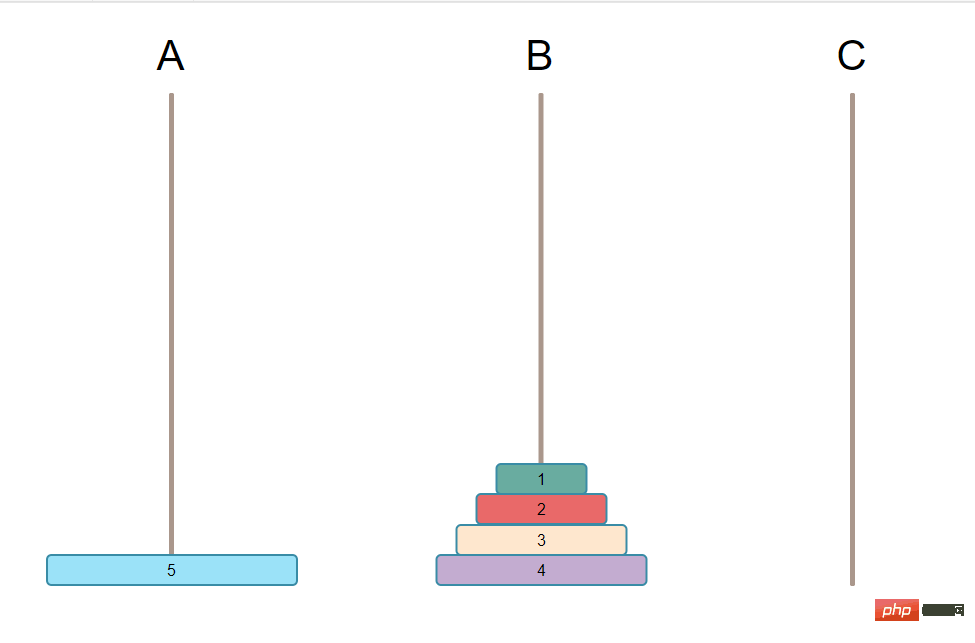
第二步把A上第 N 个盘子（也就是最大号盘子）移动到C上。

这个就很简单了把，只要一步，把最大号盘子从A移动到C就可以了。如下图：

第二步

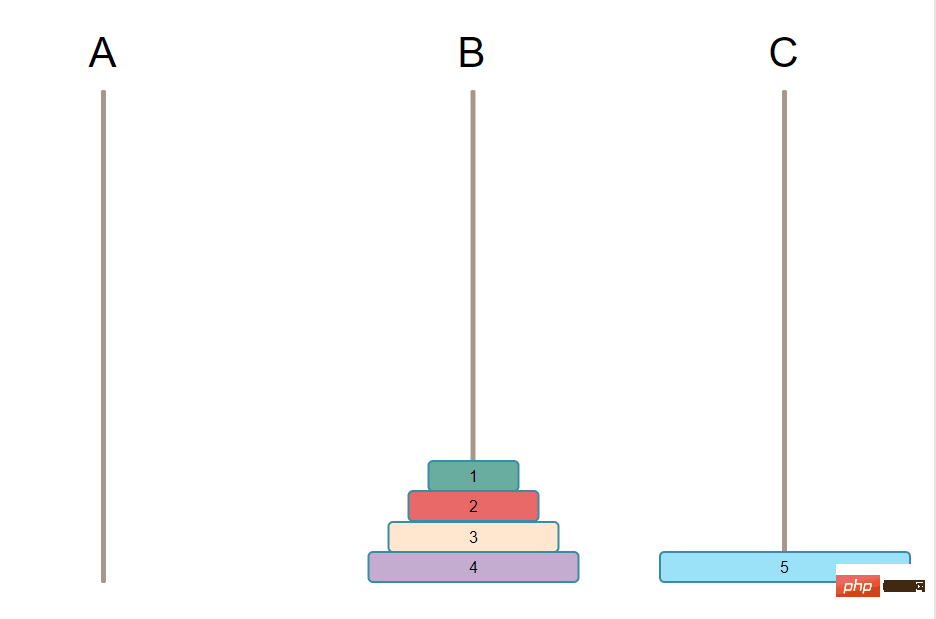
第三步把B上 N-1 个盘子移动到C上。

注意：要实现把 N-1 个盘子移动到C，是不是又变成了找出其中最大盘子，然后先移动最大盘子。所以这里的话其实就变成了重复第 1，2步骤，从这 N-1 个中找出最大的先移动到C，循环往复。

那第三步其实就等于变更了需求假设 K = N – 1。
B柱子上有K个盘子，A柱子是空的，C柱子有最大的盘子所以对于K个盘子的B柱子而言等同于空。
第一步把B上 K-1 个盘子移动到A上。
第二步把B上第 K 个盘子移动到C上。
第三步把A上 K-1 个盘子移动到C上。
…

就变为了下图

先找到剩余的盘子中最大的

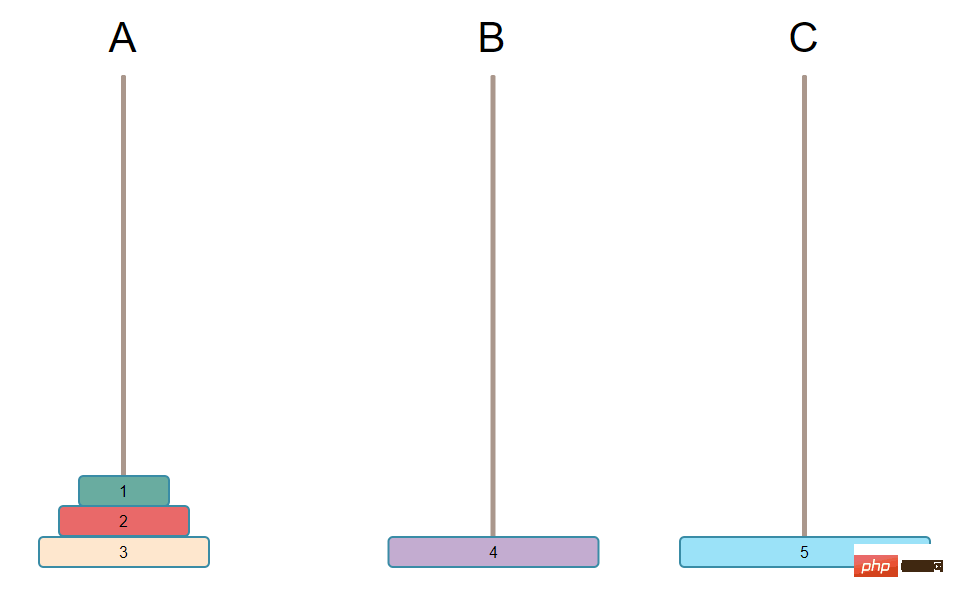
然后移动最大号盘子

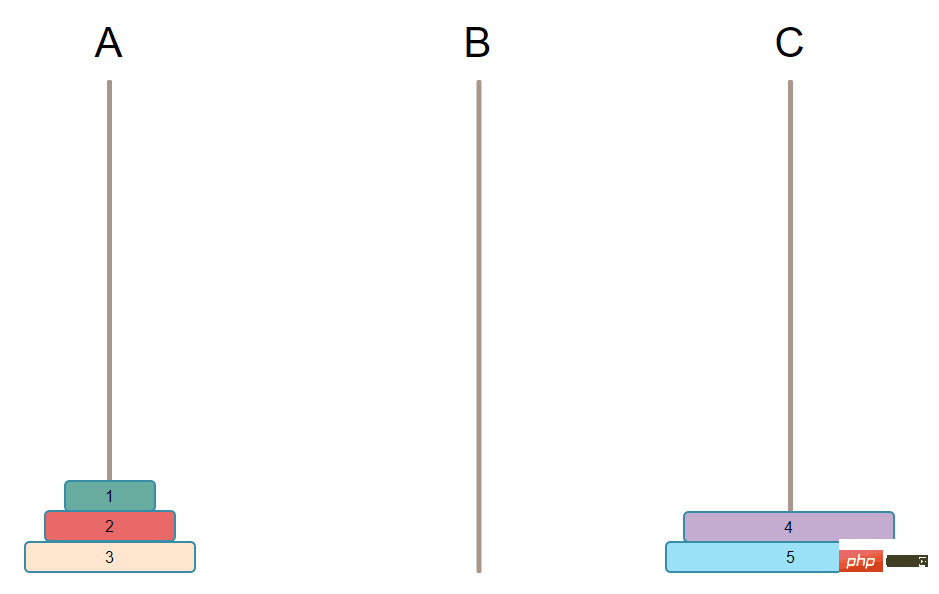
然后循环下去直到只剩一个盘子，直接移动到C，游戏结束。

辅助柱子

什么是辅助柱子？假设你现在所有待移动的盘子都在A上，目标是移动到C上，那么B就是 N-1 个盘子的辅助柱子。因为他们只能暂存在这里，不然就不满足游戏规则了。

这里需要先找出辅助柱子，不要想怎么实现，先理清逻辑。

要实现从A移动到B，那么C就是辅助柱子
要实现从A移动到C，那么B就是辅助柱子
要实现从B移动到C，那么A就是辅助柱子

实现

通过上面的分析可以看到这其实就是一个循环往复的重复操作，很类似递归，所有这里可以使用递归来实现。

要使用递归需要有2个必要条件

1.求出递推公式
2.找到退出条件

退出条件很好写，肯定是只有一个盘子的时候，直接移动到C柱子上。

那么递推公式是什么呢？还是根据上面的逻辑分析，可以分解为3步。

第一步把【N-1个】盘子先从A移动到B
第二步把【第N个】盘子从A移动到C
第三步把【剩下的N-1个】盘子从B移动到C

下面是PHP实现的伪代码：

class HanoiTower
{
    // 计数器
    public $count = 0;
    /**
     * 汉诺塔实现
     * 
     * @param $n 盘子号
     * @param $A 初始柱子
     * @param $B 中转站
     * @param $C 目标柱子
     */
    public function hanoi($n, $A, $B, $C)
    {
        if ($n == 1) {
            // 退出条件 只剩一个盘子的时候直接从A移动到C
            $this->biggestOne($n, $A, $B, $C);
        } else {
            // 第一步把 【n-1】 个盘子从A移动到B 此时C为中转站
            $this->hanoi($n - 1, $A, $C, $B);
            // 第二步把 【第n】 个盘子从A移动到C
            $this->biggestOne($n, $A, $B, $C);
            // 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
            $this->hanoi($n - 1, $B, $A, $C);
        }
    }
    /**
     * 移动最大的盘子
     * 直接从A移动到C
     */
    public function biggestOne($n, $A, $B, $C)
    {
        ++$this->count;
        echo '第', $this->count, '步 ', '把 ', $n, '从 ', $A, '移动到', $C, '<br />';
    }
}
$n = 5;
$hanoiTower = new HanoiTower();
echo '这是一个有 【', $n, '】 个盘子的汉诺塔：', '<br />';
// 调用执行
$hanoiTower->hanoi($n, 'A', 'B', 'C');
echo '总共需要走：【', $hanoiTower->count, '】 步';

结果如下：

以上就是解析PHP如何实现有趣的汉诺塔算法的详细内容，更多请关注php中文网其它相关文章！

声明：本文转载于：learnku，如有侵犯，请联系admin@php.cn删除

解析PHP如何实现有趣的汉诺塔算法

起源

分析

辅助柱子

实现

发表回复 取消回复

发表回复取消回复