生活中，我们用肉眼分辨为美的事物，常常神奇地包含了黄金分割比，此时就不得不感叹一下：数学的美丽无处不在。而黄金分割数列（又称斐波那契数列）的后一项与前一项比值的极限就是二分之根号五减一，约等于0.618（即黄金分割比例）。那么使用PHP要如何实现黄金分割数列呢，不急，我们慢慢来了解。

首先我们来了解一下黄金分割数列（即斐波那契数列）：

斐波那契数列指的是这样一个数列：

1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765…….

即：前两个值都为1，从第三位开始，每一位都是当前位前两位的和

规律公式为：

Fn = F(n-1) + F(n+1)

• F：指当前这个数列

• n：指数列的下标

好了，了解了黄金分割数列（斐波那契数列），下面我们来了解一下使用PHP实现的方法。

方法1：利用数组

观察上面给出的数列，结合数组知识，可以分析出：

• 数组下标为0或1时，元素的值为1；

• 数组下标为2时，元素是a[0]+a[1];

• 数组下标为3时，元素是a[1]+a[2];

• …..

• 数组下标为n时，元素是a[n-2]+a[n-1];

可以得出：

• a[0]=1

• a[1]=2

• a[n]=a[n-2]+a[n-1] （n>2）

代码实现：

<?php
header("Content-type:text/html;charset=utf-8");
function test($num){
    $arr=[];
    for($i=0;$i<$num;$i++)
    {
        if($i==0 || $i==1){
            $arr[$i]=1;
        }else{
            $arr[$i]=$arr[$i-1]+$arr[$i-2];
        }
		echo $arr[$i]." ";
    }
}
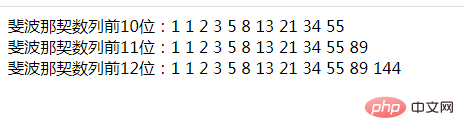
echo "斐波那契数列前10位：";
test(10);
echo "<br>斐波那契数列前11位：";
test(11);
echo "<br>斐波那契数列前12位：";
test(12);
?>

输出：

了解了如何利用数组来求斐波那契数列，下面我们来看看利用递归来求斐波那契数列。

方法2：使用递归

<?php
header("Content-type:text/html;charset=utf-8");
function fbnq($n) {
	if ($n <= 0) {
		return 0;
	}
	if ($n == 1 || $n == 2) {
		return 1;
	}
	return fbnq($n - 1) + fbnq($n - 2);
}

echo "斐波那契数列第10位：" . fbnq(10);
echo "<br>斐波那契数列第11位：" . fbnq(11);
echo "<br>斐波那契数列第12位：" . fbnq(12);
?>

输出：

递归法也实现出来了，是不是很简单！

递归算法可以将一个负责的问题使用较短的代码将问题解决出来，但是运行的效率比较低。

好了就说到这里了，有其他想知道的，可以点击这个哦。→ →php视频教程

以上就是PHP和黄金分割数列的完美邂逅（不可错过）的详细内容，更多请关注php中文网其它相关文章！

声明：本文原创发布php中文网，转载请注明出处，感谢您的尊重！如有疑问，请联系admin@php.cn处理

https://www.php.cn/php-weizijiaocheng-480698.html